BP算法

BP算法是由学习过程由信号的正向传播与误差的反向传播两个过程组成。由于多层前馈网络的训练经常采用误差反向传播算法，人们也常把将多层前馈网络直接称为BP网络。

1. 人工神经元

神经网络中最基本的成分是神经元(neuron)模型，在生物神经网络中，每个神经元与其他神经元相连，当 它 “兴奋”时, 就会向相连的神经元发送化学物质，从而改变这些神经元内的电位；如果某神经元的电位超过了一个“阈值”(threshold)，那么它就会被激活，即 “兴奋” 起来，向其他神经元发送化学物质。

1943 [McCulloch and Pitts, 1943]将上述情形抽象为如下图所示的简单模型，这就是一直沿用至今的“M -P 神经元模型”。在这个模型中，神经元接 收到来自几个其他神经元传递过来的输入信号，这些输入信号通过带权重的连 接(connection)进行传递，神经元接收到的总输入值将与神经元的阈值进行比较，然后通过“激活函数”(activation function)处理以产生神经元的输出。把许多个这样的神经元按一定的层次结构连接起来，就得到了神经网络。

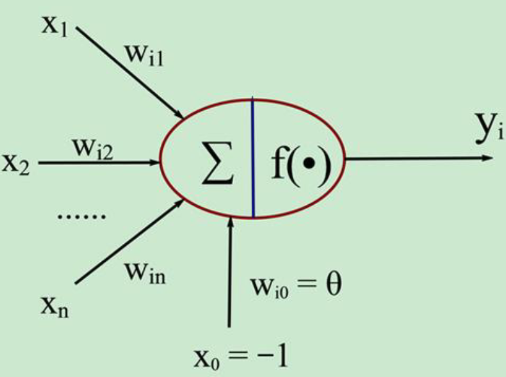
图中$x_i \sim x_n$是从其他神经元传来的输入信号，$w_{ij}$表示从神经元$j$到神经元$i$的连接权值，$\theta$表示一个阈值，那么神经元$i$的输出与输入的关系表示为
$$
net_i=\sum_{j=1}^nw_{ij}x_j-\theta
$$

$$
y_i=f(net_i)
$$

式中$y_i$表示神经元$i$的输出，函数f成为激活函数或转移函数。如果将阈值看成是神经元$i$的一个输入$x_0$的权重$w_{i0}$，则上述公式可以简化为
$$
net_i=\sum_{j=0}^n w_{ij}x_j
$$
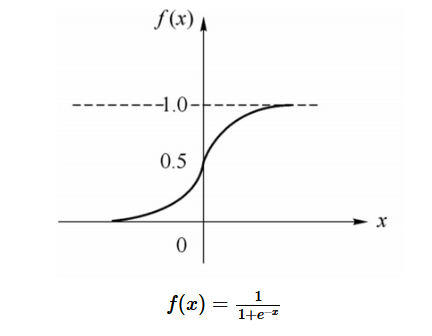
选择的激活函数不同，$y_i$的取值范围也不同，而函数f通常要求选择可微的函数，通常选择Sigmoid函数
$$
sigmoid function：f(x)=\frac{1}{1+e^{-x}}
$$
函数图像如下所示。该函数具有以下特性：非线性、单调性、无限次可微，并且当权值很大时可近似阈值函数，当权值很小时可近似线性函数。

2. 前馈神经网络

构成前馈神经网络的神经元接受前一级输入，并输出到下一级，无反馈。其节点分为两类:输入节点与计算单元。每个计算单元可有任意个输入，但只有一个输出，而输出可耦合到任意多个其他节点的输入。前馈网络通常分为不同的层，第$i$层的输入只与第$i–1$层的输出相联。输入节点为第一层。输入和输出节点由于可与外界相连，称为可见层，而其他的中间层则称为隐藏层。而其中三层前馈网络又是其特例，三层前馈网络由输入层、中间层和输出层构成，有两个计算层，也称三层感知器，能够求解非线性问题。三层或三层以上的前馈网络通常又被叫做多层感知器(Multi-Layer Perceptron，简称MLP)，由三部分组成：一组感知单元组成输入层；一层或多层计算节点的隐藏层；一层计算节点的输出层。多层感知器的表示：输入节点数-第1隐层节点数-第⒉隐层节点数-…-输出节点数。

当使用阈值函数作为神经元输出函数时，任何逻辑函数都可以使用一个三层的前馈网络实现。当神经元的输出函数为Sigmoid函数时,上述结论可以推广到连续的非线性函数。在很宽松的条件下，三层前馈网络可以逼近任意的多元非线性函数，突破了二层前馈网络线性可分的限制。

要使神经元合理的组合输出，需要先让其学习以模拟生物的学习过程。神经元的学习算法通常采用Hebb学习规则，如果神经元$u_i$接收来自另一神经元$u_j$的输出，则当这两个神经元同时兴奋时，从$u_j$到$u_i$;的权值$w_{ij}$就得到加强。具体到前述的神经元模型，可以将Hebb规则表现为如下的算法$\Delta w_i=\eta yx_i$。式中$\Delta w_i$是对第$i$个权值的修正量，$\eta$是控制学习速度的系数。太大会影响训练的稳定性，太小则使训练的收敛速度变慢，一般取$0<\eta≤1$，人工神经网络首先要以一定的学习准则进行学习，然后才能工作。

3. BP算法

三层前馈网络的适用范围大大超过二层前馈网络，但学习算法较为复杂，主要困难是中间的隐藏层不直接与外界连接，无法直接计算其误差。而BP算法可解决这一问题。其主要思想是从后向前(反向)逐层传播输出层的误差，以间接算出隐藏层误差。因此算法分为两个阶段:

• 第一阶段(正向传导过程)：输入信息从输入层经隐藏层逐层计算各单元的输出值;
• 第二阶段(反向传播过程)：输出误差逐层向前算出隐藏层各单元的误差，并用此误差修正前层权值。

在反向传播算法中通常采用梯度法修正权值，为此要求输出函数可微，通常采用Sigmoid函数作为输出函数。下面考虑一个三层前馈网络，其中$i$表示前层第$i$个单元，$k$表示后层第$k$个单元，$O_j$表示本层的输出，$w_{ij}$表示前层到本层的权值，$w_{jk}$表示本层到后层的权值。其中的输出函数选择Sigmoid函数。

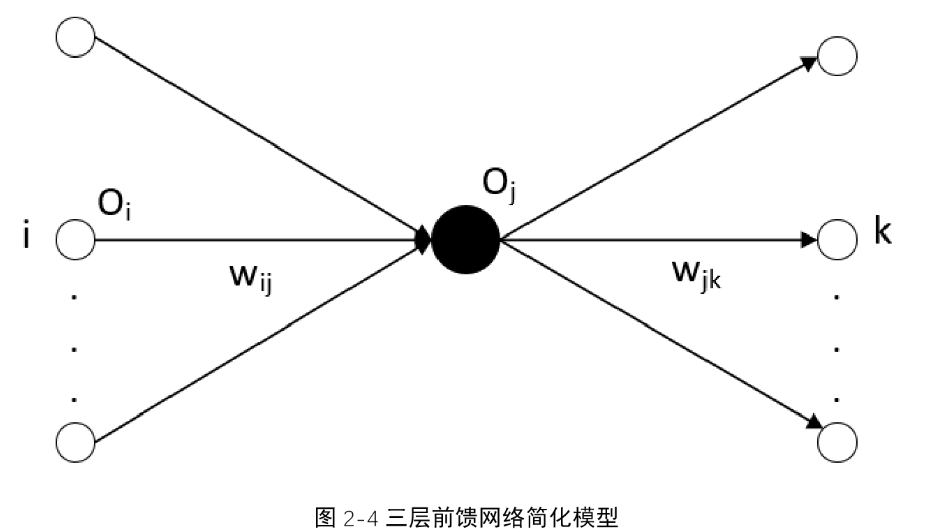
第一阶段的正向传导过程中，第$j$层的输入如此按公式所述，第一阶段从输入层逐层往后计算输出，直到最后一层。
$$
net_j=\sum_{i=0}^nw_{ij}O_i
$$

$$
O_j=f(net_j)=\frac{1}{1+e^{-net_j}}
$$

第二阶段的反向传播过程中，对于输出层，$O_k$是实际输出，与理想输出$y_k$的均方误差可以通过以下公式计算。
$$
E=\frac{1}{2}\sum_k(y_k-O_k)^2
$$
输出层的局部梯度为：
$$
\delta_j=\frac{\partial E}{\partial \ net_j}=\frac{\partial E}{\partial \ out_j}\frac{\partial\ out_j}{\partial \ net_j }=-(y_j-O_j)O_j(1-O_j)
$$
因此计算权值对误差的影响如下公式所示
$$
\frac{\partial E}{\partial \ w_{ij}}=\frac{\partial E}{\partial \ net_j}\frac{\partial \ net_j}{\partial \ w_{ij}}=\delta_jO_j
$$
采用负梯度修正权值，
$$
w=w-\delta ·O
$$
BP算法易形成局部极小而得不到全局最优，训练次数多使得学习效率低，存在收敛速度慢等问题。

传统的BP算法改进主要有两类：

• 启发式算法：如附加动量法，自适应算法。
• 数值优化算法：如共轭梯度法、牛顿迭代法等。

算法流程：

对每个训练样例,，BP算法执行以下操作：先将输入示例提供给输入层神经元，然后逐层将信号前传，直到产生输出层的结果；然后计算输出层的误差(第4-5行)，再将误差逆向传播至隐层神经元(第6行)，最后根据隐层神经元的误差来对连接权和阈值进行调整(第7行)。该迭代过程循环进行，直到达到某些停止条件为止，例如训练误差已达到一个很小的值。

但我们上面介绍的“标准BP算法”每次仅针对一个训练样例更新连接权和阈值，也就是说，图中算法的更新规则是基于单个的$E_k$推导而得。如果类似地推导出基于累积误差最小化的更新规则，就得到了累积误差逆传播(accumulated error backpropagation)算法。累积BP算法与标准BP算法都很常用。一般来说,标准BP算法每次更新只针对单个样例，参数更新得非常频繁，而且对不同样例进行更新的效果可能出现“抵消”现象。因此，为了达到同样的累积误差极小点，标准BP算法往往需进行更多次数的迭代。累积BP算法直接针对累积误差最小化，它在读取整个训练集D一遍后才对参数进行更新，其参数更新的频率低得多。但在很多任务中,累积误差下降到一定程度之后,进一步下降会非常缓慢，这时标准BP往往会更快获得较好的解，尤其是在训练集D非常大时更明显。